One-Dimensional Wave Function: Born’s Rule, Sandwich Integral and Overlap Rules

Question:
At time t=0 a particle is described by the one-dimensional wave function

where k and α are real positive constants.

(a) State Born’s rule in the context of one-dimensional wave mechanics and explain why this rule leads to the requirement for wave functions to be normalized. Verify that the wave function Ψ(x, 0) in Equation 1 is normalized.

(b) Write down the sandwich integral rule for the expectation value of momentum. Hence find the expectation value of the momentum, < p_x >, in the state described by Ψ(x, 0).

(c) Given that in the state described by Ψ(x, 0), what is the uncertainty of the momentum, ∆p_x, in this state?

(d) Suppose that the particle is in a potential energy well with the normalized ground-state energy eigenfunction

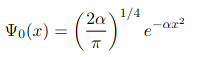
and corresponding energy eigenvalue E₀. Use the overlap rule to find the probability that a measurement of the particle’s energy at time t=0 will give the ground-state energy, E₀. (Your answer should be a function of α and k.)

Order step by step solution of this question written in pdf format:

For any inquiry about this solution before and/or after purchase please fill in the following form and submit it to Detailed Solution.