Metric Tensor
Different points of a Riemannian space, communicate to each other and it is possible to write a equation which describes the relation between two given neighbor points’ properties. This equation is called metric:

where dS2 ( or line element) is the square of space-time interval between two neighbor points; dS2 is a scalar and invariant under coordinate transformation. Defined in a coordinate system, dxμ are the components of a contravariant vector that connects these two points. In addition to the differences between components, any displacement between two points is dependent on the positions of them in the coordinate system, through the function gμν (x), which is a covariant tensor of rank-2, called the metric tensor.
In a Cartesian (rectangular) coordinate system because of the homogeneity, displacement between two points is independent of their components; and for a rectangular coordinate system build in Minkowski space-time, metric is defined as :

where ξμ are the space-time rectangular coordinate components and ξ i are only spatial parts of them; c is the speed of light; ημν is the metric tensor for this case and its matrix representation is:

The components of gμν in a curved coordinate system can be found through coordinate transformation from rectangular coordinate system, ημν , to the curved one; but rectangular coordinate system exists only in flat space-time (Minkowski space-time). It is impossible to construct rectangular coordinate system in a curved space-time; in the other words, curvature is obstruction to move from a curved coordinate to a rectangular one; but it is possible to do that locally if space-time is locally flat.
Metric transformation from a rectangular coordinate system, ξ , defined locally in a point of a curved space-time, to a curved coordinate system, X , can be written as:

So we can find the local values of metric tensor; but it is impossible to find its global value, except when the local curvature is the same at all points of the space-time.
Three important properties of metric tensor are as follows:
• gμν is symmetric.
• determinant of gμν is not zero. So inverse matrix, g μν exists, that is the contravariant form of metric tensor; so we have:

• metric tensors can be used to lowering or raising indices.
Equations of Motion
In a co-moving rectangular coordinate system attached to a particle (with non zero mass), the velocity of the particle is:
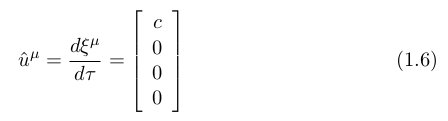
Where τ is the proper time, which is a parameter along space-time curve of the particle.
The velocity of the particle can be transformed into a curved coordinates through its expansion on curved coordinates components:

where ![]() is the four-velocity of particle in curved coordinate system (X).
is the four-velocity of particle in curved coordinate system (X).
ûμ is constant, so ![]() , and we have:
, and we have:

where,

are the Christoffel symbols; they describe the changes of the metric tensor under motion between different points of a coordinate system; they vanish in rectangular coordinate system. Christoffel symbols are in fact objects that give us covariant derivatives of tensors; the term covariant here refers to covariant under coordinate transformation; so covariant derivative of a tensor is a tensor. Ordinary derivatives of tensors do not transform tensorially, so they are not tensors. By writing coordinate transformation of vector Aμ , it is easy to show that its covariant derivative is:

where Aμ,λ = ∂Aμ /∂Xλ is the ordinary derivative of Aμ in the X coordinate system.
Equations(1.8) are equations of motion and they describe geodesics (extremal curves) in Riemannian space-time, where there is at least one geodesic in order to move from a point to the another one; in fact a geodesic is the trajectory of a freely moving particle; that is straight a line in Minkowski space-time.
We can show that the equations of the motion represent covariant derivative of vector dXα /dτ ; so we have:

This is the covariant derivative of four-velocity which is zero; so it vanishes in all the coordinate systems.
Some properties of the Christoffel symbols: Christoffel symbols are not tensor ( they are just functions of metric); they are symmetric under lower indices ( Γαμν = Γανμ ).
Space-Time Curvature
Riemann’s curvature tensor:
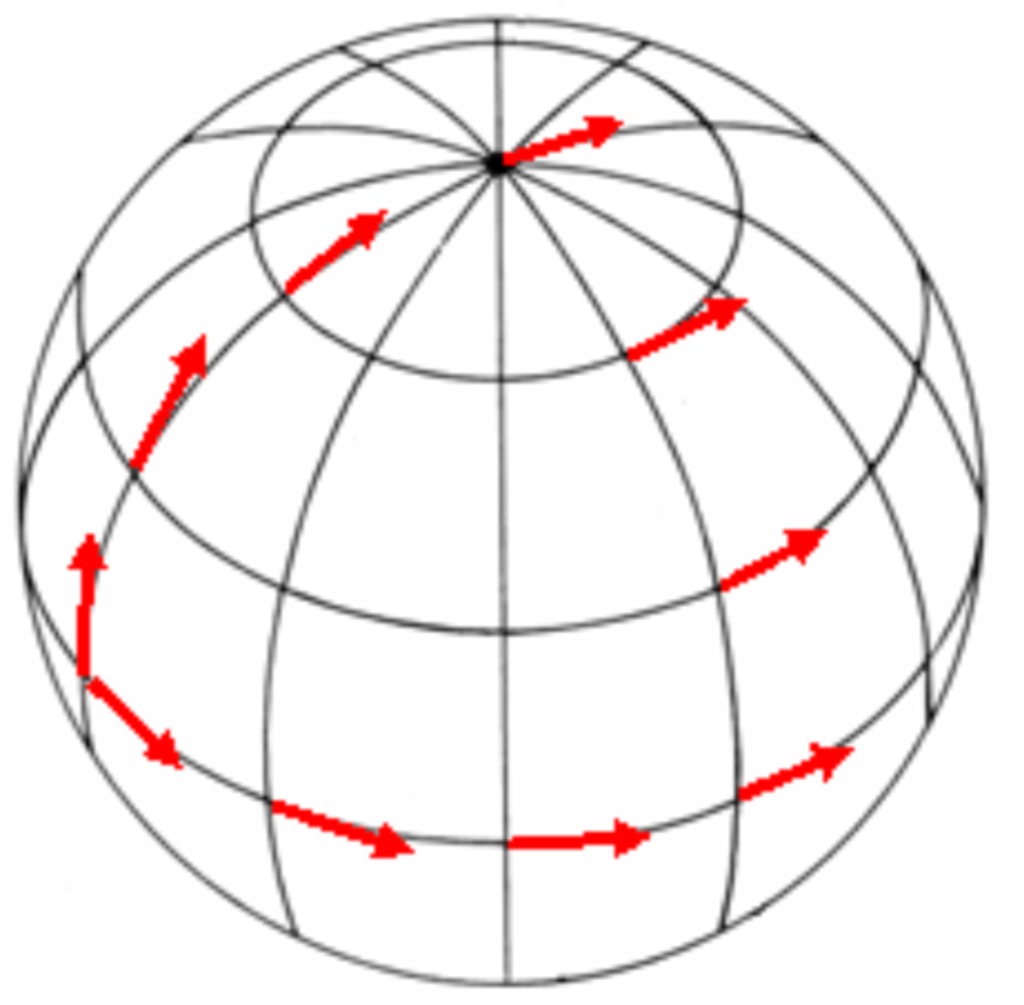
space.
After parallel transportation of a vector, v μ along a loop, its direction changes if the surface inside the loop, is curved; the changes of v μ is dependent on the area inside loop, its curvature and the vector itself:

Rμναβ represents the curvature of the surface inside loop; and it is called Riemann’s curvature tensor and it can be written as:

Ricci curvature tensor:
The contraction of Riemann’s curvature tensor gives the Ricci curvature tensor as:
Rμν =Rαμαν (1.11)
or in more practical form:

Ricci scalar:
The contraction of Ricci tensor; gives Ricci scalar: R= Rμμ = gμνRμν (1.13)
Bianchi identity:
Riemann’s curvature tensors obey the relation below that is called Bianchi identity:
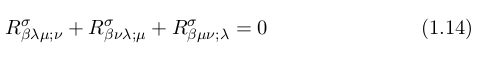
Einstein’s curvature tensor:
From the Bianchi identity we can find the relation below:

So we found a tensor of rank-2 that its covariant derivative is zero. This tensor is called Einstein’s curvature tensor:

after multiplying it to the metric tensor, it can be written as:
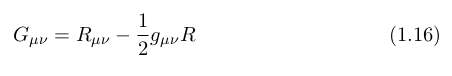
Because its covariant derivative is zero, the Einstein’s curvature tensor is conserved under coordinate transformations.
Einstein Field Equation
The equation which relates curvature of the space-time to the matter and its motion, is known as Einstein field equation and it can be written as:
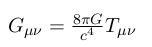
In this equation Gμν is the Einstein’s curvature tensor and G is the gravitational constant where its value is about:
G~6.674×10-11 Nm2kg-2
Tμν is the energy-momentum tensor; it contains all the properties of a fluid that change the shape of the space-time. Energy-momentum tensor of a perfect fluid, that is a fluid without viscosity, is given by:

where ρ is the fluid density and p is its stress, measured in the fluid’s comoving coordinate system (rest frame). uμ are the covariant components of the four-velocity in a arbitrary coordinate system.
Because of the conservation of the Einstein’s curvature tensor, Gμν , the energy-momentum tensor, Tμν , is conserved under coordinate transformations, that means:
(Tμν );μ = 0
that is the generalization of conservation laws of energy and momentum.