What is Cosmology?
Cosmology is the study of the universe as a whole; it deals with the mechanism of the evolution of the universe and its components.
According to the modern cosmology, universe begins with a Big Bang; and through the evolution, different fields split from each other and the components of the universe evolve. While the universe expands, different structures (such as galaxies, black holes, stars and planets) emerge.
In order to study the universe we need to know its space-time geometry, and its components (or fluids) and how the fluids interact with each other and with space-time.

( https://www.google.com)
Cosmological Principle and RW-Metric
The most fundamental principle in the universe is the cosmological principle that is made of two symmetry assumptions as follows:
1• Universe is homogeneous in large scale. This means the properties of the universe are the same in any given point; so from a given observation point, the density is independent of the distance from the observer.
2• Universe is isotropic. This means the properties of the universe are the same in all directions, so there is not any preferred observer in the universe and the observer sees the same density in all directions.
According to the cosmological principle the local curvature must be the same at all points of the universe. The line element for this universe can be written as:

that is called Robertson-Walker (RW) line element; where (r,θ, φ) are spatial comoving coordinates and, t is the cosmic time. As a function of cosmic time the factor a(t) is called scale factor which represents the expansion of the universe; K is the curvature parameter and can be taken -1, 0, +1. When K=1 universe is closed without boundary and its spatial shape is a sphere with radius a(t) at time t; but when K=0 the universe is flat and infinite with Euclidean space (flat infinite slices of space through the arrow of cosmic time); for K=-1, universe is open and infinite, but its spatial geometry is hyperbolic. From the equation above, the RW-metric tensor is:

Friedmann Equations and our Flat Universe
In order to find Einstein’s curvature tensor and field equation for a space-time defined by Robertson-Walker metric, at first we need to find Non-zero components of Ricci curvature tensor after finding Christoffel symbols from Robertson-Walker metric tensor. Non-zero components of Ricci curvature tensor are as follows:

and from them Ricci scalar is:
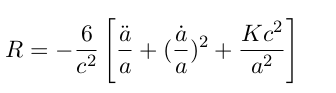
These relations give us the non-zero components of Einstein’s curvature tensor, Gμν , in the co-moving coordinate system defined by Robertson-Walker metric where a given particle or fluid is at rest. By substituting energy-momentum components, Tμν , and the components of Gμν , in Einstein’s field equations, we can find Einstein’s field equations for this system:


These are called the first and second Friedmann’s equations. H(t) defined by:

is called Hubble parameter. It gives us the expansion rate of the universe at a given cosmic time, t, and its present value,H0 = H(t0 ), is called Hubble constant. According to the latest observations carried by the ESA’s Planck satellite, the value of the Hubble constant is about:
H0=67.3 ± 1.2 km/s /Mpc ; Mpc = 3.09 × 1019 km = 3.26 × 106 light-year
When K=0 , universe is flat and the first Friedmann’s equation can be simplified as:

where ρc (t) is the critical mass/energy density of the universe at a given cosmic time; the critical mass/energy density of the universe changes as the Hubble parameter evolves over time and it defines the curvature of the universe at any given time. If the total mass/energy density (the sum of density of different types of fluids ) of the universe is bigger or smaller than the critical mass/energy density at a given time, universe is curved at that time; for the bigger total mass/energy density than the critical one, universe is closed without boundary (spherical space), and for the smaller values of the total mass/energy density universe is open and infinite (hyperbolic space). Today’s value of the critical mass/energy density ρc (t0 ) is:

Observations show that today’s value of total mass/energy density of the universe is very close to this critical value, so we live in a flat universe.
The ratio of the energy density of a fluid (radiation, dark matter, baryonic matter and dark energy ) in the universe to the critical energy density is called density parameter of the fluid, Ωfluid . So the total energy density parameter of the universe, Ωtotal , which is the ratio of total mass/energy density of the universe to its critical mass/energy density, represents the curvature of the universe. So today’s value of the Ωtotal (or Ω0 ) that is the sum of today’s values of mass/energy density parameters of radiation, dark matter, baryonic matter and dark energy, is equal to one.

Fluids
- Baryonic Matter
Although baryons and bosons are different particles, in astronomy and cosmology the term baryonic matter or bosonic matter refers to the ordinary matter that emits or absorbs light; so it can be detected by its emitted radiation. Black holes are also considered as ordinary matter.
2. Radiation
Radiation includes all the particles with relativistic velocities, in the universe (photons and particles with velocities very close to the light).
3. Dark energy
Dark energy is a hypothesized term given to a mysterious force which accelerates the expansion of the universe; hence it works like antigravity. While gravity is an attractive force which draws mass together in a very local level, dark energy is a repulsive force that pushes things away from each other on large scales…..find more
4. Dark Matter
Astronomers have observed that the motion of stars in galaxies is more different than they would if the only source of gravity was ordinary visible matter made up stars, our solar system and everything which is detectable by its interaction with electromagnetic waves. So in addition to ordinary matter there must be another source of gravity which cannot emit or absorb light; it is called dark matter. According to the observations made by astronomers, the mass of dark matter must be about ten times of ordinary matter to explain strange behavior of stars. For instance on the edges of the galaxies stars move so fast that they would scape from the gravitational pull of galaxies if there wasn’t any dark matter inside galaxies.
Dark matter make up about 22 percent of the mass of the universe, while the visible ordinary matter contributes almost 4 percent of it; in fact dark matter and dark energy together made up most of the stuffs of the universe; that is about 96 percent. But dark energy and dark matter are different things hypothesized to explain different phenomena. Cosmologists are not sure what is dark matter. But there are different proposals about the nature of dark matter, for instance theoretical particles known as weakly interacting massive particles (WIMPs).
Evolution of the Fluids
Universe is an isolated system and it expands adiabatically; so its heat content is constant (or δQ = 0, if Q is the heat content of the universe). On the other hand all the processes in the universe are reversible; so the second law of thermodynamics can be written as:
T dS = δQ
where S is the entropy and T is temperature. So universe is an isentropic system, this means that:
T dS = dE + pdV = 0
Where E is internal energy, p is pressure, and V is the volume. But the linear expansion of the homogeneous and isotropic universe demands that, E = ρc2 V , and, V∝ a3 . Scale factor, a and, mass/energy density, ρ are functions of time only; so we have:

This is the continuity equation which gives evolution of the mass/energy density through the expansion of the universe.
Both the pressure and the mass/energy density appear in this equation and the second Friedmann equation; so it is useful to define the equation of state that is a equation between these two parameters given by:
p = wρc2
where w has different values for different fluids. When the fluid is pressure-less (i.e. dust, baryonic and cold dark matter), w=0 ; and for radiation, w = 1/3 .
By substituting P = wρc2 in continuity equation, we can find that:

where γ=w+1.
In this equation ρ and a are the mass/energy density and the scale factor, at a given time; but ρ0 and a0 are their today’s values, respectively.
Standard Cosmological Model
Flat universe that is isotropic and homogeneous in large scales, and contains radiation, dark matter, ordinary (or baryonic) matter, and cosmological constant, is occasionally called standard cosmological model or the concordance cosmology. According to this model our universe began with a Big Bang approximately 13.81 billion years ago. The very early universe just after the Big Bang, was dominated by radiation; then matter (dark and baryonic) appears in our universe; as time goes on density of the matter decreases gradually while the cosmological constant (or vacuum energy) increases; so the large amount of mass/energy density of today’s universe is cosmological constant, and it’s going to dominate the future of our universe. The first Friedmann’s equation (or constraint equation) of this model is
H2 = H02 ( Ωr,0 a−4 + Ωdm,0 a−3 + Ωbm,0 a−3 + ΩΛ,0 )
in this relation Ωr,0 , Ωdm,0 , Ωbm,0 , and ΩΛ,0 , are today’s density parameters of radiation, dark matter, baryonic matter and cosmological constant, respectively. According to the latest observations carried by the ESA’s Planck satellite, their values are as follows:
Ωr,0 ∼ 10-5
Ωdm,0 =0.268
Ωbm,0 =0.049
ΩΛ,0 =0.683
and H0=67.3 ± 1.2 km/s /Mpc , is the Hubble constant.
Cosmic Redshift
Because of the expansion of the universe the wavelength of a light after emitting from a point (star) in the universe, increases. So when it reaches to an observer, it has a longer wavelength than it had at emission point. Light moves along a path defined by ds2 = 0; by applying this relation to the Robertson-Walker line element and ignoring the contribution of peculiar velocity of the source point, we can find that:

where z is a parameter, common for measuring the cosmic redshift; a(te) is the scale factor of universe when the light emitted and λe is the wavelength at emission point; a(to) is the scale factor of the universe at the observation point and λo is the wavelength of the light when observed. Today’s value of scale factor is given by a0 = 1, so the equation above will be simplified for today’s observations (when to = t0 ) :

Proper Distance
The proper distance (or physical distance) is the spatial distance between any two events when the events are simultaneous (this distance is in fact spatial geodesic). The proper distance of a emission point from an observer, is given by:

and its today’s value (when a(to ) = a(t0) = 1), is called co-moving proper distance (because it is measured at a fixed time, that is today).
Horizons
In the universe, according to the general theory of relativity, nothing can travel faster than the speed of light; and because of that the regions of the universe from which, we can receive information, is limited by event and particle horizons:
•Event horizon
we are limited by the event horizon in order to observe all the events in our future. The proper distance to the event horizon at time t, is given by:

which has different values for different models of universe and its today’s value can be found for t=t0. So the events that happens today, at distances larger than dpEH(t0), will not be viewed in the future.
•Particle horizon:
we cannot observe all the events happened in the past. The particle horizon defines our observable universe by the proper distance given by:

Where t is the observation time and tmin is the smallest time of universe. For the cosmological models with Big Bang, tmin=0, and similar to the event horizon, today’s proper distance to the particle horizon is dpPH(t0) that is in fact the size of our observable universe today.