Question:
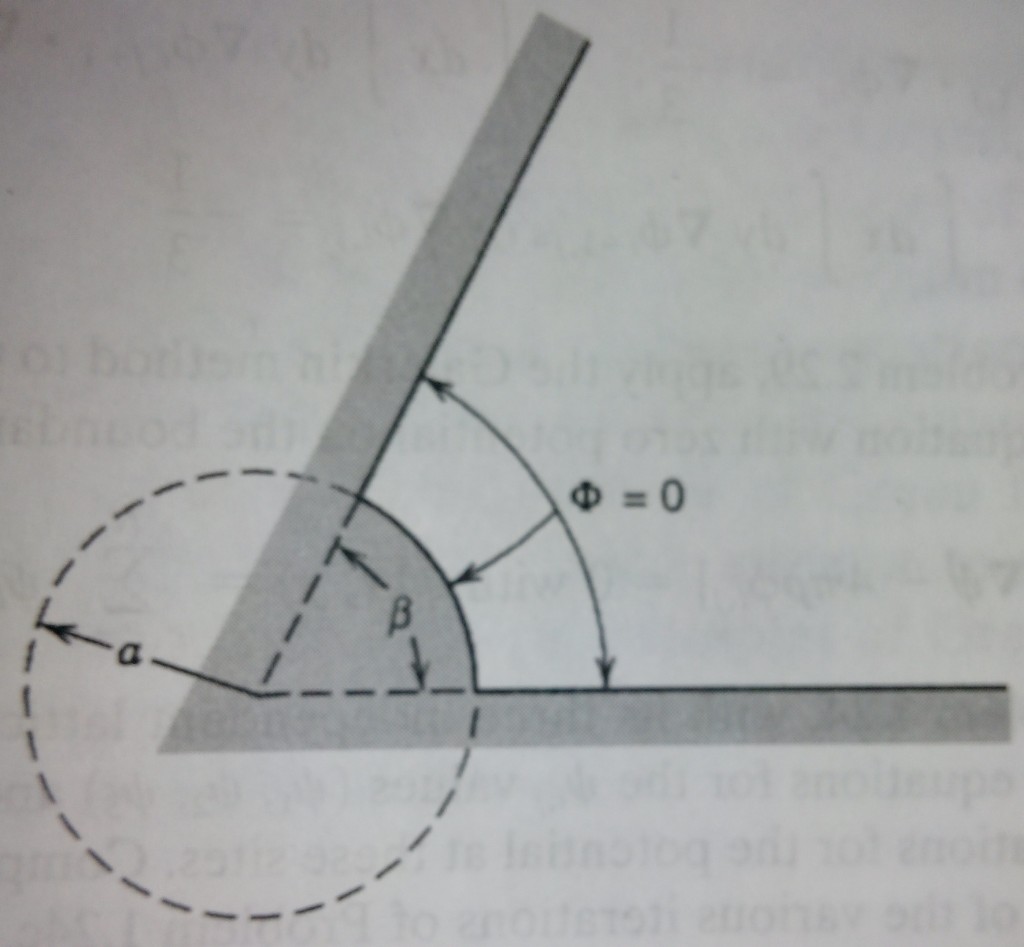
The two-dimensional region, ρ ≥ a, 0 ≤ φ ≤ β, is bounded by conducting surfaces at φ = 0, ρ = a, and φ = β held at zero potential, as indicated in the sketch.
At large ρ the potential is determined
by some configuration of charges
and/or conductors at fixed potentials.
(a) Write down a solution for the potential Φ(ρ, φ) that satisfies the boundary conditions for finite ρ.
(b) Keeping only the lowest nonvanishing terms, calculate the electric field components E ρ and E φ and also the surface-charge densities σ(ρ, 0), σ(ρ, β), and σ(ρ, φ) on the three boundary surfaces.
Solution:
(a) Inside the region bounded by ρ ≥ a, 0 ≤ φ ≤ β surfaces, where there isn’t any electric charge and current, potential is given by Laplace equation, i.e.,
∇2Φ = 0
In two dimension, in terms of the polar coordinates (ρ, φ), this equation can be written as,
Order step by step solution of this problem written in pdf format:
Solution ID: ElecMag-J2-26
Solution of this problem will be sent to your email account within 8 hours.
$49.99
For any inquiry about this solution before and/or after purchase please fill in the following form and submit it to Detailed Solution.